Singular matrix in fem solve
It seems that you always have to use the GMRES solver, the LU solver usually fails with a singular matrix. The simple examples that I looked at use it and they fail if you change it to LU.
Why is this?
In the case of 5g1 (according to VJ) it's because the wrong pressure basis function has been used. (see also comments below)
Make sure you have the correct basis specfied in all places that it's required. Specifying the wrong basis for the pressure field can cause this error.
I have a test problem with a 6 element tricubic mesh that solves, but when I split one of the rectangular/cube elements into two triangular wedge elements and add versions I get a singular matrix. I think this has something to do with the the boundary conditions, but I'm not sure how to go about diagnosing the problem.
What is the best way to inspect the matrices? Is there an example of how to do this somewhere? There are some options during 'define solve' that control matrix output. Is 'fem write matrix' helpful?
>>Warning: Volume at ng= X ne= X less than zero
update: This is caused by an element becoming inverted. One possible cause is when using collapsed nodes and there is a wrinkle near a collapsed node. See UsingVersions for a discussion of this.
What do you do when you get the warning message: >>Warning: Volume at ng= X ne= X less than zero ? this warning occurs sometimes when attempting to solve a finite elasticity problem, and is usually followed by the problem failing to solve.
According to the comment in fe50/ZERE50.f, where the message comes from, it is triggered when the determinant of the deformation gradient, DET(DZDX), ie the volume, is less than 0.
In the problem I am trying to solve I get this error when I have collapsed nodes in the mesh.
I have a simplified test case with plain hexahedral elements that solves OK, but the mesh I want use to has some elements split into 2 using collapsed nodes and versions as shown in the image below.
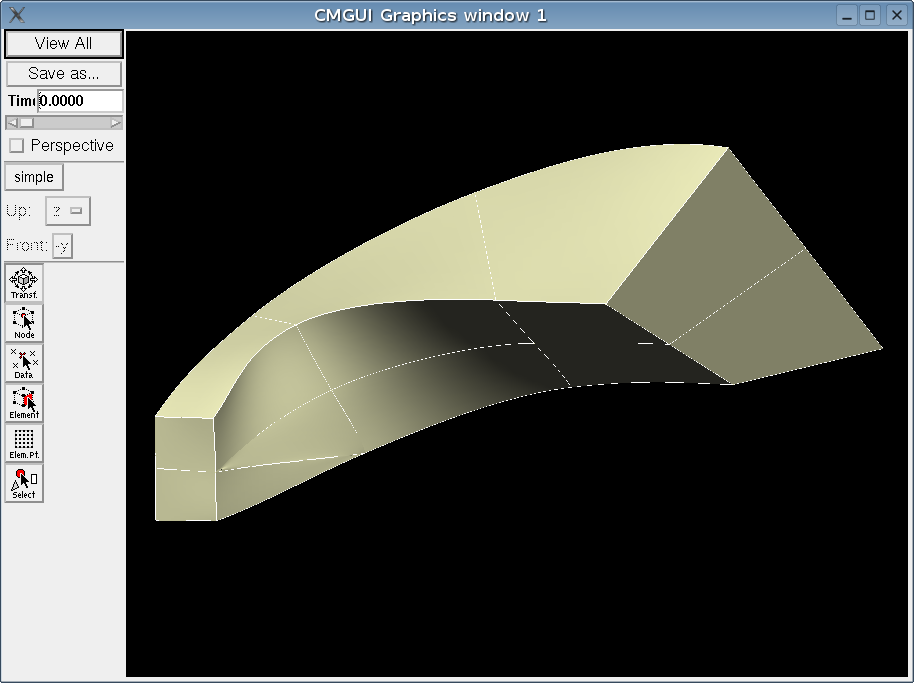
The warning happens when using this mesh with everything else the same as the case without the collapsed nodes that works OK.
The command causing the warning is fem solve inc 0.
How is the volume becoming less than zero if there is no deformation?
How do I diagnose the problem and fix it? How is the volume becoming less than zero if there is no deformation?
The finite difference calculation of derivatives of the stiffness matrix may "deform" the mesh.
