UsingVersions
When creating a cubic hermite mesh that uses collapsed elements there are several issues to consider regarding the use of versions.
Conditions under which this advice is relevant
- the mesh uses cubic hermite basis functions
- an element has at least one collapsed edge
- the collapsed node has at least 2 versions
- the collapsed element has an adjacent element in same direction as the collapsed line
- the mesh use the rectangular cartesian coordinate system
Symptoms of incorrect version design
- in cmgui there is a "wrinkle" at the collapsed node
- in cm, there are numerical problems when attempting to solve an elasticity problem, e.g. volume less than zero, singular matrix, non-convergence
The cause of the symptoms mentioned above
The wrong interpolation formula is being used in the collapsed element.
The standard cubic interpolation formula between two nodes is a function of the position and first derivative at each node (e.g. Bradley1997, eqn 3 ), however when the element contains a collapsed node then the derivative in the collapsed direction is not defined and therefore should not be part of the interpolation. This is described in Bradley1997 by equations 13-16.
Discussion
The reason why this problem is not evident in some meshes is that when the derivative in the collapsed direction is set to zero then that term is excluded from the standard interpolation formula and the formula works fine.
Examples of this are the collapsed element in example 21h that has no adjacent elements and the apex of the rectangular cartesian heart mesh. In these cases there are no adjacent elements that use the derivative in the collapsed direction and it remains set to zero in all versions of the node and the correct interpolation function is used.
In a case where there are one or more elements adjacent to the collapsed element in the collapsed direction and the same version is used in the adjacent element(s) then the derivative of the relevant versions in the collapsed direction may be set to a non-zero value for a better representation in the adjacent element. If the standard interpolation formula is used for the collapsed element then these derivative values will be used and the wrong interpolation will result. If a different version is used in the adjacent element then the derivative value can be set appropriately in each element (but there will not necessarily be C1 continuity).
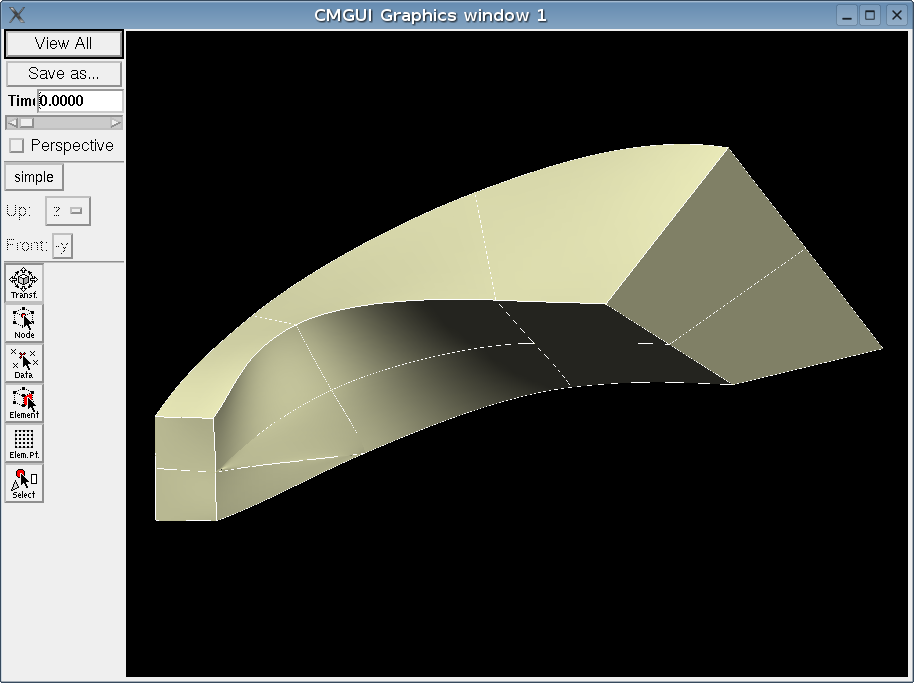
The image below shows a case where the incorrect number of versions has been used. 2 have been used at the collpased nodes where 4 are required to provide sufficient degrees of freedom to allow different interpolation to be used in the collapsed elements and the adjacent uncollapsed elements.
Example
Example 151 demonstrates some aspects which should be considered when using collapsed elements.
References
Bradley1997: Bradley, C.; Pullan, A. & Hunter, P. Geometric modelling of the human torso using cubic hermite elements. Annals of Biomedical Engineering, 1997, 25, 96-111
